Homography
Apr 8, 2021 opencv camera image homography
Math is beautiful when not seen as just equations. Homography is one of the beautiful concepts in planar geometry. Lets consider a physical point P\(( x, y)\) is represented in two different images as \(( x_{1}, y_{1})\) and \(( x_{2}, y_{2})\).
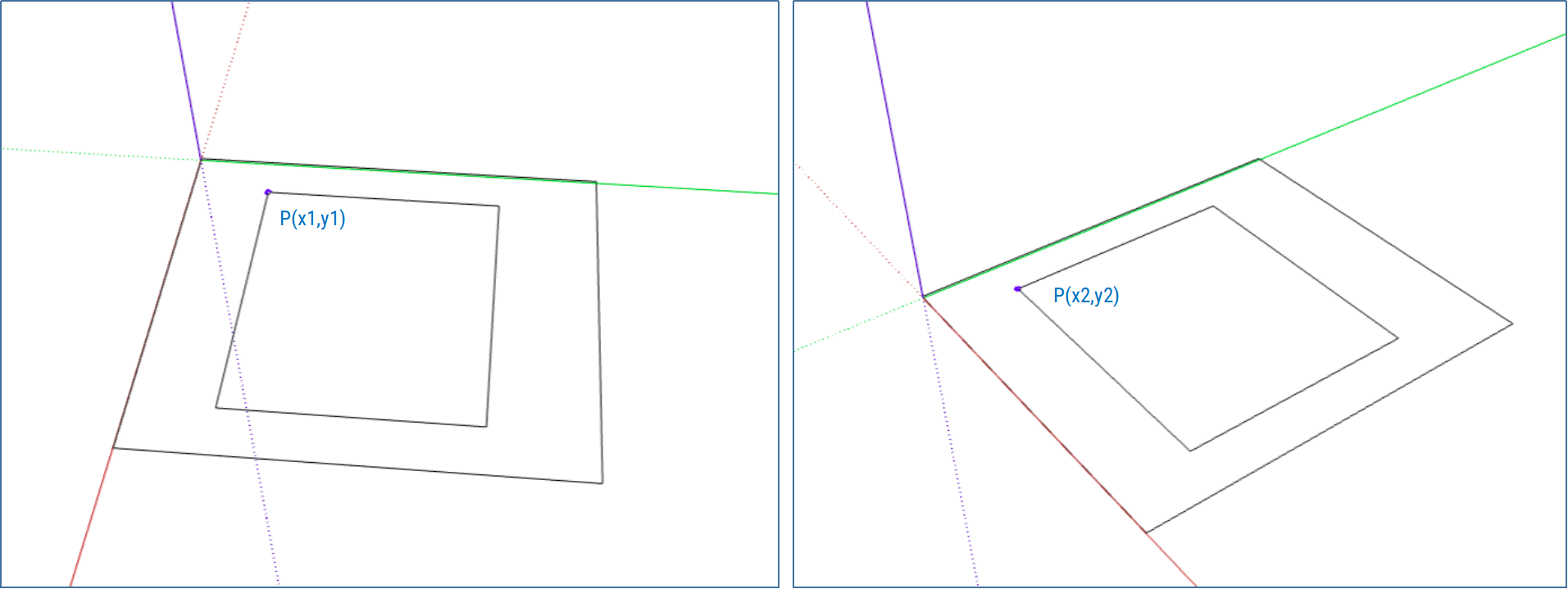
Here homography H can be considered a 3x3 matrix which relates a point \(( x_{1}, y_{1})\) to the same point in another image \(( x_{2}, y_{2})\)
\[H = \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix}\]We can express this as
\[\begin{bmatrix} x_{1} \\ y_{1} \\ 1 \end{bmatrix} = H \begin{bmatrix} x_{2} \\ y_{2} \\ 1 \end{bmatrix}\] \[\begin{bmatrix} x_{1} \\ y_{1} \\ 1 \end{bmatrix} = \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix} \begin{bmatrix} x_{2} \\ y_{2} \\ 1 \end{bmatrix}\]If we have this Homography matrix, we can apply to every pixels in the first image to generate the second image, of a scene. This transformation creates a warped image.